BaekJoon : 1629번(곱셈)

Java : BaekJoon Divide And Conquer

BaekJoon Divide And Conquer(분할 정복) 저의 문제풀이 입니다.
핵심 부분은 Bold해 놓겠습니다!

혹시 더 좋은 방법 알려주신다면 정말 감사하겠습니다!

1629

자연수 A를 B번 곱한 수를 알고 싶다. 단 구하려는 수가 매우 커질 수 있으므로 이를 C로 나눈 나머지를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.

10 11 12

출력

첫째 줄에 A를 B번 곱한 수를 C로 나눈 나머지를 출력한다.

4

분할 정복

A, B, C는 모두 2,147,483,647 이하의 자연수이기 때문에 A를 B번 거듭제곱 해주면 A,B가 2,147,483,647일 때, 시간 초과가 날 수 밖에 없습니다. 그렇기 때문에 단순히 거듭제곱하기 보다는 지수 법칙과 모듈러 성질을 이용해 분할 정복으로 문제를 해결할 수 있습니다.

지수 법칙

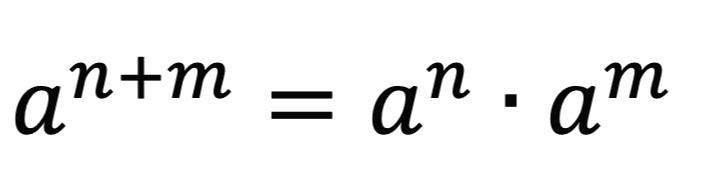
지수 법칙을 이용하면 a⁸일 때,

a⁸ -> a⁴ * a⁴
a⁴ -> a² * a²
a² -> a¹ * a¹

위와 같이 분할할 수 있습니다. 이 때, 지수가 짝수가 아닌, 홀수일 때는

a¹¹ -> a⁵ * a⁵ * a¹
a⁵ -> a² * a² * a¹
a² -> a¹ * a¹

위와 같이 분할하게 됩니다.

모듈러 성질

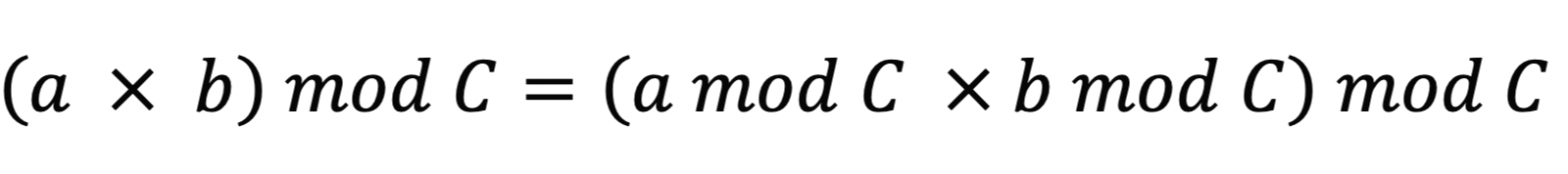
모듈러 성질을 이용해 자료형 범위를 넘어서지 않게 답을 구할 수 있는데, 이 때, 2,147,483,647(2³¹-1) * 2,147,483,647(2³¹-1) 은 long 자료형 범위 2⁶⁴-1를 넘지 않는다는 것을 이용할 수 있습니다.

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
	static long a;
	static long b;
	static long c;
	
	public static long partition(long num) {
		// 지수가 1일 때
		if(num == 1)
			return a % c;
			
		// 재귀를 이용해 분할 정복을 실행 합니다.
		long tmp = partition(num / 2);
		
		// tmp * tmp는 long 자료형 범위를 넘지 않기 때문에 tmp 하나당 % c를 해주지 않아도 됩니다.
		long result = tmp * tmp % c;
		
		// 지수가 홀수 일 때, a를 한번 더 곱해 줍니다. ex) a9 = a4 * a4 * a1
		if(num % 2 == 1) 
			result = result * a % c;
		
		return result;
	}
	
	public static void main(String[] args) {
		InputStreamReader isr = new InputStreamReader(System.in);
		BufferedReader br = new BufferedReader(isr);
		
		try {
			StringTokenizer stk = new StringTokenizer(br.readLine());

			a = Long.parseLong(stk.nextToken());
			b = Long.parseLong(stk.nextToken());
			c = Long.parseLong(stk.nextToken());
			
			System.out.println(partition(b));
			
		} catch (Exception e) {
			e.printStackTrace();
		}
	}
}

---

해당 코드들은 저의 GitHub에서 확인할 수 있습니다.